女科技人的美麗心世界 Taiwan Women e Press

在這個大數據的時代，人人都想有一些數據的基本功夫。大數據、數據分析、人工智能、腦神經網路、深度學習，都是大數據時代越來越重要的技能。然而，聽起來好玄、好深奧難懂，似乎不是一般人能輕易了解的。

做為美國歷史最悠久的威廉瑪麗學院 MBA 商管碩士班數據分析必修課程的教授，我常常要思考該怎麼樣讓來自各行各業的學生，能夠在最短的時間內，有效、迅速的理解並運用數據分析的核心觀念。

數據分析俗稱統計學，是數學的一個分支。它的美，來自於優雅簡潔的數學方程式。然而，如果這些概念僅以方程式和符號的形式呈現，這樣的抽象表示即便非常簡潔，大多數人卻很難真正的理解它們在日常中的實際應用。有好多常見提問，例如：偏差 （deviation） 與標準差 （standard diviation, ?） 是否相同？標準差與標準分數（standard score, Z） 有何不同？標準誤差（standard error）呢？這是一種特殊類型的誤差（?） 嗎？誤差不也叫殘差 （residual） 嗎？為什麼每樣東西都有一個希臘字母名稱？最重要的是，標準差的用途何在？能當飯吃嗎？企業真的能使用標準差來賺錢嗎？

許多學生都需要修統計課程，優秀的學生會努力學習一系列的希臘字母，逼迫自己記住一系列公式，然後考個高分，日後才能順利申請上一間頂尖大學。可惜的是，廣大優秀學子學習統計學的大部分精力，可能都花在理解艱澀的希臘字母和數學方程式上，而很少於實際中應用。幾年後他們實際記住了多少，或是可以在日常專業上實際應用多少統計知識，那就完全是另外一回事了。這是很可惜的，因為統計數據是如此實用的工具，可以在很多方面使用。例如，工廠製程中的品質管理、Netflix 影片推薦和谷歌廣告，都可以通過統計分析來幫企業賺大錢，香港賭馬大王 Bill Benter 也是靠數據分析成為賭馬界的東方不敗及億萬富翁。

教學多年來，我發現使用來自房地產網站 Zillow 的房地產數據設計的課堂活動，最能讓學生輕鬆又有效率地學習數據分析的核心概念。我的 MBA 數據分析和 MSBA 機器學習課程的第一個作業，是讓每個學生在 Zillow 網站上，於學校位處的威廉斯堡，選擇一棟她們喜歡的房子，請學生將所選房子以數據手工輸入到一個簡單的網路表單裡，這樣一來，所有學生所選房子的地產資料都被編譯至一個 Google sheets 資料檔案，然後我們用這個數據檔案來做各式各樣的課堂討論練習。

例如，表 1 為最近一年學生們所選房產資料的一部分。這些數據資料包括了分類變量（categorical variables，例如郵遞區號）和數字變量（numeric variables，例如價格）。大多數財務數據總是存在偏差，價格也不例外，這讓我們有機會討論處理偏差的各種方法。我們可以使用同一個數據集資料檔案，通過對分類變量和數值變量不同的排列組合，來進行各種分析。接下來一個月左右的時間裡，我們會以不同的方式分析數據集並計算數值。我們幾乎可以使用這個數據集資料檔，完成一整個學期的數據分析入門課程。

在數據檔案中，學生可以清楚的看到她們自己的名字與全班的數據表，我會請每個學生在自己的圓形便利貼上，寫下個人姓名、原始分數（例如屋齡）、偏差和 Z 分數（即標準分數）。接著與全班一起討論：誰的 Z 分數為 1.96？誰在3以上？低於-3？誰的分數為零？誰在 95% 的信賴區間（confidence interval）內？誰在外面？

我總是會邀請全班同學來到白板前，並使用她們的數據點一起構建直方圖（histogram）（圖 2）。這個練習是動態的、有趣的和參與性的。學生獨力地構建一個數據點，然後整個班一起建構直方圖，這親身的經驗強化了上面說過的，基本但重要的統計概念。學生可以清楚地看到她們在分佈上的位置，她們在直方圖上的位置如何以 Z 分數反映，以及偏差如何表示她們與班級平均值的關係。全班還可以一起計算整筆資料的方差、標準偏差、偏度和其他性質。這對於幫助學生區分語言上令人困惑的術語特別有效，例如（案例的）偏差與（樣本的）標準偏差，以及（案例的）標準分數與（樣本的）標準偏差。它還能用來深入了解案例和數據集之間的關係。在親身的實踐活動之後，我繼續演示如何使用各種軟體（例如 Google Sheets、JASP 和 Tableau）在電腦上創建直方圖。學生可以清楚地看到，電腦軟體只是將手動創建直方圖的程序自動化了。

在討論相關性（correlation）時，我再次要求學生製作「數據點」，但這次用她們自己的數據記錄來記錄兩個變量，而不是一個變量（例如，臥房數，以及衛浴數），學生們也會寫下這兩個變量的 Z 分數，然後將它們相乘。之後全班的分數加起來平均一下就是皮爾森積差相關係數（Pearson Correlation ）r。學生將她們的數據點貼在白板上，一起構建全班的散佈圖（scatter plot）。然後，我們可以使用散佈圖來討論迴歸（regression）、殘差（residual）、模型擬合（model fit）及預測模型的其他重要概念（圖 3）。

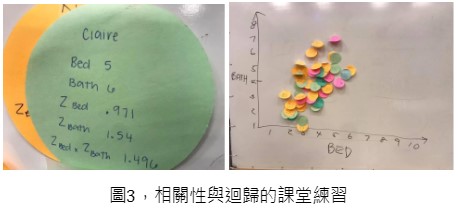
房地產數據集是一個很好的教學工具，主要有兩個原因： (1) 普通人很容易獲得相關的領域知識。例如，大多數人直觀地理解更大的房子（即更大的平面面積）可能會更貴，而增加衛浴數可能會增加房產的價值。此外，（2）變量之間的關係通常非常強且可預測。例如，例如，臥室數量總是與浴室數量高度相關，老師不用擔心分析結果不顯著。每個額外的臥房總是會為房產增加可觀的價值，因此我們可以指望迴歸模型的貝塔係數（β係數）一定是顯著且為正值的。因此，教師們不必擔心在新的一學期分析結果會不會不一樣。

最重要的是，Zillow 使用他們的數據集生成 Zestimate，這是一種預測模型或機器學習預測的實際應用，用於估計財產價值（Schneider 2019）。從概念上講，Zestimate 類似於房產估價的概念，這對於大多數人（包括我們的學生）來說都是淺顯易懂的。然而，很少有人會立即認為他們知道如何自己創建Zestimate 估算值。當學生在學習了線性迴歸模型後，就會意識到她們馬上可以理解和自己設計 Zestimate 模型，而且馬上獲得很大的成就感。可以建立她們自己的 Zestimate 方程式，做出自己的房價預測。也可以馬上看出，如果房子多一間臥房，價值會上漲多少，或者如果房子從一個郵遞區號搬到另一個，價值會下降多少。這些簡單、生動和直觀的練習，使相當抽象的概念和希臘字母（例如，β）更容易消化，記住與應用。

這個教室裡的活動過程不僅對於理解預測模型的和評估預測模型性能的方法極為重要，當我們一起研究 Zillow 網站時，學生更了解預測模型如何在現實世界中運用。

總而言之，數據分析，通常稱為統計，由於其眾多的行話、符號和晦澀的術語而令人生畏。通過讓學生參與手動組合房地產數據集的過程，使這些抽象和技術概念更加具體和平易近人，便能既簡單又有趣。